第2部分 基础篇 第2章 密码技术（2）

2.2.2. 加密解密算法

小云：首先我们学习加密解密算法。现代密码学的基础是加密解密算法，它的安全性是通过算法所依赖的数学问题来保证的。

小天：《算法设计与分析》这门课看起来很重要，不多当时学起来的确难。

小云：哈哈同感。密码学源于古希腊时期，很久以来，人类使用的加密解密机制基本都是对称加密，直到上世纪70年代，非对称加密算法才诞生。两种机制的主要区别在于加密解密过程中使用的密钥是否相同，也分别适用不同场景下的加密解密需求。

2.2.2.1. 对称加密算法

小云：对。对称加密算法对于用户数较少，加密数据量较大的加密场景中，计算量较小，效率非常高。

小天：那么对称加密算法有哪些呢？

小云：根据算法对明文信息的处理方式，可以把对称加密算法分为两类：分组密码和流密码。分组密码是把明文信息分组为数据块（block），用同一密钥算法对每一块加密，输出也是固定长度的密文，多用于网络加密。典型的分组算法有MD5，DES，3DES，AES，IDEA以及国密算法中的SM-1，SM-4，SM-7。其中MD5、DES和3DES因为安全和效率原因已经被淘汰。国际上常用的是AES算法。

第二类是流密码，又称序列密码，加密时每次加密一比特位或一个字节的明文，明文和密钥按比特位对其做约定的运算，即可获得密文。流加密是一种快捷高效的加密方法，但其安全性较低。 比较著名的流密码有RC4和GSM和国密算法中的ZUC祖冲之算法。

• AES加密算法

小天：AES算法听说过，可以详细介绍一下。

小云：好的，对称密码在用的不多了，AES算法算一个。从1997年开始，美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）开始组织遴选DES的替代者，称之为AES（高级加密标准），历时三年，经过多次算法大会评选，2001年底从15个候选算法中选出Rijndael作为AES，公布为美国国家标准FIPS-197，供免费试用。

小明：那它的加密机制是什么呢？

小云：该加密算法采用对称分组密码体制，分组长度128位，也就是说，每个分组为16个字节（每个字节8位）。密钥长度支持128比特、192比特、256比特，密钥的长度不同，推荐加密轮数也不同。比如密钥长度128比特，加密轮数为10轮，就是说一个明文分组会被加密10轮。明文分组一般使用字节为单位的正方形矩阵描述，称为状态矩阵。在算法的每一轮中，状态矩阵的内容不断发生变化，最后的结果作为密文输出。AES解密过程仍为10轮，每一轮的操作是加密操作的逆操作。AES的特点是速度快，整个过程可用数学描述。

小云：对称加密算法我们就不过多介绍了。下面学习一下非对称加密算法。

2.2.2.2. 非对称加密算法

小云：非对称加密算法是密码技术发展的重大突破，具有里程碑式的意义。我们常说的公钥密码机制，其实所指的算法就是非对称加密算法。

小明：哦。主要有哪些呢？

小云：主要有RSA、背包密码、McEliece密码、Diffe_Hellman、Rabin、零知识证明、椭圆曲线乘法（ECC）、EIGamal算法等。我们本节重点介绍下RSA和ECC。

• RSA算法

小云：1976年，Diffie和Hellman提出公钥密码机制后，1977年，Ron Rivest、Adi Shamirh和LenAdleman在麻省理工学院共同开发出RSA非对称加密算法。三人因此获得2001年图灵奖。

小明：我也听说过，RSA是第一个成熟的公钥算法，也是目前最有影响力的公钥加密算法，那么基本原理是什么？

小云：RSA算法中的公钥和私钥是一对大素数（十进制100~200位，甚至更大）的函数，从公钥和密文恢复明文等同于对两个大素数的乘积进行因式分解。它能够抵抗现有的已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。

小天：主要用途是？

小云：RSA可以被用于公钥密码和数字签名。

小明：我还听说量子计算机对RSA密码造成威胁的事情，这个是什么情况？

小云：对，有这么回事。2019年底，由于谷歌量子计算机技术的突破，量子计算机使用shor算法威胁RSA密钥机制一时成为热门话题。理论上，如果存在对大素数进行质因数分解的高效算法，那么RSA的安全体系将会彻底坍塌。另外还存在的威胁是暴力猜解，也就是逐个尝试可能的值。

当前生产环境中RSA随机数的值都是1024比特，其乘积形成的N值长度达到2048比特，这个也是NIST SP8000-57建议在2030年之前可用的安全长度，对于经典计算机包括超级计算机来说，对这个N值得因数分解需要的计算量非常惊人，计算时长估计需要80年。对于量子计算机来说，以Google 宣布的54个量子比特（实际使用53个量子比特）组成的量子计算机Sycamore为例，只需要200秒，就能实现了超级计算机1万年的计算量，应该不是难事。

小明：这么说还真是存在风险。

小云：对，不过从当前现实来看，量子计算机量子比特数进展缓慢，噪声过多，纠错处理难度较大，shor量子算法成功的概率还有待提高。并且随着量子比特数量提升，技术难度和制造成本将会呈指数级增长，这也为加密算法的进一步发展赢得了时间，一些抗量子攻击的算法也已经出现，并在不断完善。

小云：我们再说说椭圆曲线密码算法。

• 椭圆曲线密码（ECC，Elliptic Curves Cryptography）

小明：与RSA相比，椭圆曲线算法有哪些优势呢？

小云：与其他密码算法相比，ECC的优势是可以实现密钥更短，却能提供相当的或更高等级的安全，比如ECC的224-255比特位就相当于RSA 2048比特位长度的同等强度。所以存储占用空间更小，网络带宽要求更低，处理速读更快。

小云：椭圆曲线是Koblitz和Miller两人于1985年同时提出的。ECC是利用椭圆曲线实现的密码技术的统称，实际上包括三部分内容：椭圆曲线公钥密码，椭圆曲线数字签名，椭圆曲线密钥交换。

小明：需要回顾一下椭圆曲线的知识。

小云：是啊，我们慢一点。一般情况下，平滑椭圆曲线可以用方程式y²=ax³+bx²+cx+d表示，其中a，b，c，d是系数。我们简化下方程式，比如a=1，b=0，c=0，d=7，得到y²=x³+7，这个就是比特币中使用的方程图像曲线（见图），也就是secp256k1曲线（2021年，比特币升级其签名算法，将ECDSA 修改为Schnorr签名算法）。

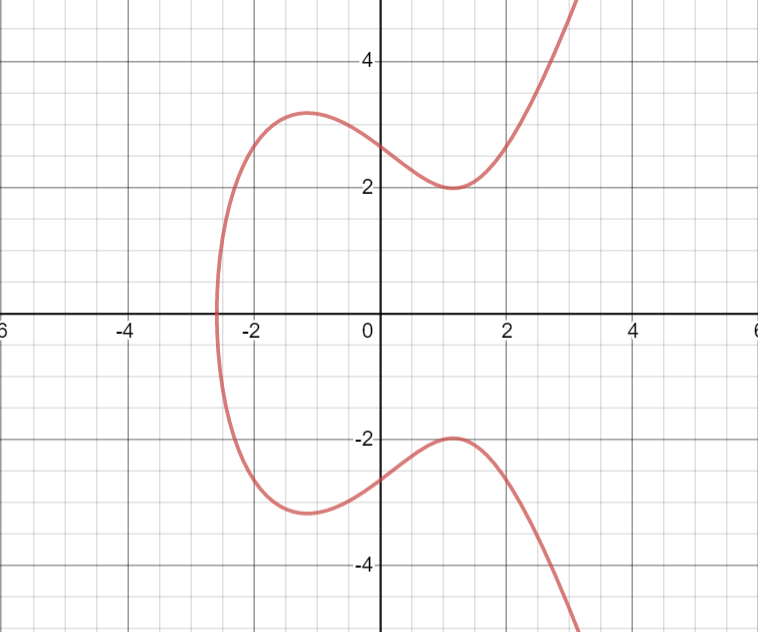
图2-4 y²=x³-4x+7的图像

小明：secp256k1代表什么？

小云：secp256k1 是SECG（高效密码组标准）协会开发的椭圆曲线签名算法标准。正是由于在比特币中使用之后，secp256k1 才逐渐被接受。secp256k1 名称的含义，其中sec 来自 SECG 标准，p 表示曲线坐标是素数域，256 表示素数是 256比特位长，k 表示它是 Koblitz 曲线的变体，1 表示它是该类型曲线中第一个标准。

小明：如何把椭圆曲线用到密码技术呢？

小云：不着急，我们先来介绍一下椭圆曲线加法运算，从加法运算来理解乘法运算，这是椭圆曲线密码学的基石。椭圆曲线的元素为椭圆曲线上的点，点的加法运算不是普遍意义的加法运算，只是一种术语，表示点相加这种运算。曲线上点的加法定义为如下的运算法则：取椭圆曲线上两点P1、P2做直线交于椭圆曲线的另一点P3，过P3做y轴的平行线交于P3`。我们规定P3`=P1+P2。（如图2-）

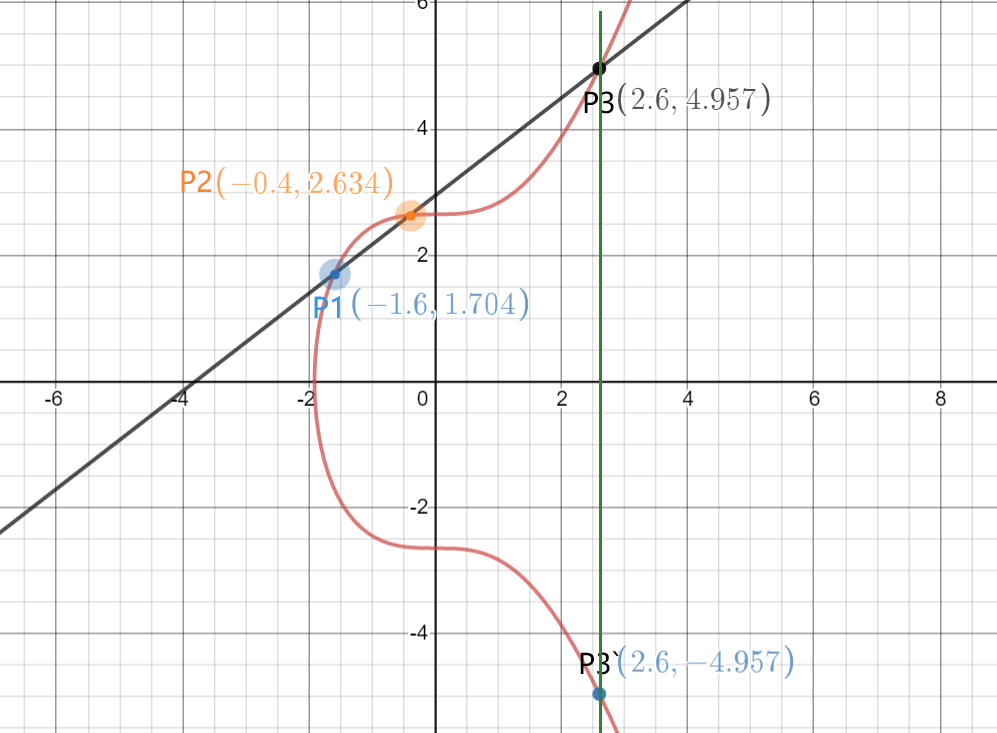
图2-5，椭圆曲线的加法。源自：https://www.desmos.com/calculator/0mnue7w8lk

小天：接下来那么乘法如何计算呢？

小云：举个例子2╳P1，其实2P1=P1+P1。根据运算法则，P1+P1计算方式就是过P1点做曲线的切线与椭圆曲线相交于点-2P1，过此点做y轴平行线与曲线的交点就是2P1。这个点2P1就是P1的2倍。如图2-。

同样道理，经过点2P1做曲线的切线与椭圆曲线相交的点是-4P1，过此点做y轴平行线与曲线的交点就是4P1。可以以此类推。

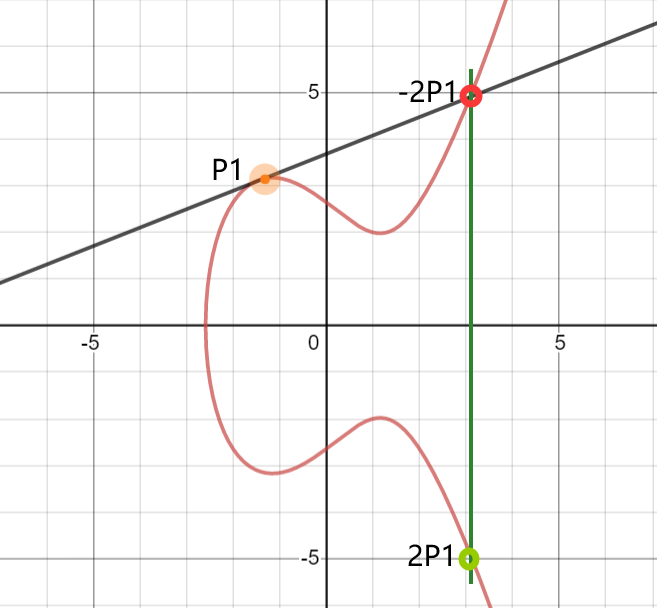
图2-6椭圆曲线乘法

小云：敲黑板了，重点来了。在椭圆曲线点的乘法运算中，已知P1和倍数（k）可以很容易计算出kP1，但是反过来，知道点P1和kP1，不可能推算出k的值。也就是说，椭圆曲线上的离散对数问题就是已知G和xG，求x，求解这样的问题非常困难。这是椭圆曲线密码的基础。再补充一下，倍数k我们可以理解为非对称加密中的私钥，它和常数点的乘积所得的值理论上就是该私钥对应的公钥（从私钥到公钥的衍生过程具体实现时故意增加了一些噪声，防止被反向破解）。

小云：我们再来回答刚才小明的问题。椭圆曲线对于非对称密码的作用体现在哪里呢？椭圆曲线非对称密码算法有两种实现，第一种是椭圆曲线Diffie-Hellman密钥交换，第二种是椭圆曲线ElGamal加密算法。

小云：我们假设你们二位，小天和小明需要通过开放网络交换对称密钥，可以使用椭圆曲线Diffie-Hellman密钥交换。

小天：好的，我们需要准备什么？

小云：每个人都要有自己的私钥和公钥，比如PRb、PUb分别是小天的公钥和私钥，PRc、PUc分别是小明的公钥和私钥，再有一个常量G。其中PUb、PUc以及常量G是可以公开发送，被别人知道的。PRb、PRc只能由所有人秘密保管，不能泄露。具体交换步骤分为：

• 小天和小明相互发送常量点G给对方。
• 接下来小天把自己的私钥与G的乘积（PRbG）也就是小天自己的公钥PUb，发给小明，同样小明把私钥与G的乘积（PRcG）也就是小明自己的公钥PUc发给小天。注意：敢把PRbG发送对方，并不怕被开放网络监听，是因为把椭圆曲线算法中的反向求解难度很大作为理论基石。
• 第三步，小天把收到的对方小明的公钥乘以自己的私钥，得到PUc*PRb,也就是(PRc*G)*PRb。同样小明把收到的对方小天的公钥乘以自己的私钥，得到PUb*PRc,也就是(PRb*G)*PRc。我们来看，(PRc*G)*PRb=(PRb*G)*PRc，双方计算结果值是相等的。这个结果值就是双方的共享密钥。

在开放网络上公开传输点G，以及小天和小明的各自公钥，可以被监听者获取，但是双方的私钥以及最后的共享密钥，却不能被破解。椭圆曲线Diffie-Hellman密钥交换的实现正是利用了椭圆曲线的离散对数难题。

小明：那么这个密钥交换能干什么呢？

小云：好的，我们可以延续你们的故事。小天要向小明发送一条消息，消息明文可以编码为椭圆曲线上的一个点M。小天将共享密钥和消息明文组装一起生成密文：PUc*PRb+M，发送给小明。该密文在开放网络上发送不会被破解。小明收到密文，从密文中减去已知的共享密钥PUb*PRc，结果就是点M，然后解码得到明文消息。这个就是椭圆曲线ElGamal加密解密算法的原理。

小天：这个明白了。还有哪些应用实现呢？

小云：还有就是椭圆曲线数字签名算法（ECDSA），这一我们在数字签名那一部分再详细介绍。明天我们学习下杂凑算法。

本文内容摘自《对话去中心化数字身份》。作者：乔布施。首发平台：https://ytm.app

欢迎转载，请注明出处及作者。