第2部分 基础篇 第2章 隐私计算技术简介(2)

2.6.3. 隐私计算技术算法理解

本聪老师：有了上面的基础知识，我们下面略微深入一些，帮助大家进一步理解。下面我们介绍一下隐私计算领域最著名的一个问题，也是不经意传输的算法实现模拟。姚期智最早在1982年提出的百万富翁问题，问题很简单，就是两个富翁想比一比谁有钱，但又不想暴露自己的财富。

小天：这个问题有意思。这个问题的一般解决办法是找个第三方进行仲裁。

本聪老师：但是这里有个前提就是每个人都不希望任何人知晓自己额财富价值。这里我们介绍解决问题的两种思路，但是都是采用叫做不经意传输的算法机制。

小明：刚才没有介绍这种算法，这里可以介绍一下吧。

本聪老师：好的，什么是不经意传输，就是消息发送者发送一些消息给接收者，但并不知道接收者具体收到了哪一条消息。好，我们回到百万富翁问题，看图2-16。我们先简化一下问题，Alice和Bob财富都是千万级别比如Alice是6千万，Bob是4千万。

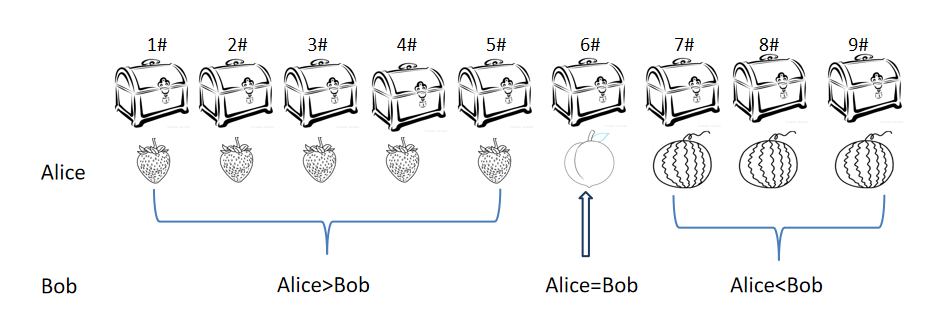
图2-16 百万富翁问题

本聪老师：我们找9个箱子，因为两人的财富都在1-9千万之间。Alice找到3种水果，分别是西瓜、桃子、草莓。她在编号数与自己财富价值最接近的箱子里放上桃子，比如6号箱子，在编号数小于自己财富价值的那些箱子里放上草莓，在编号数大于自己财富价值的那些箱子里放上西瓜。然后Alice锁上箱子，把这些箱子按照顺序给Bob。Bob只做一次选择，就是避开Alice，把编号数与自己财富价值接近的箱子，加上1把锁，然后把其他箱子全部都扔掉了。然后把Alice叫过来，一起打开箱子，注意，这时候Alice不知道Bob选择的箱子的编号，所以不知道Bob的财富，同样Bob不知道Alice对箱子进行的水果操作，所以也不知道Alice的财富。这时候打开箱子，大家觉得箱子里的水果可能会是哪个？

小天：有三种可能，是草莓，桃子或者西瓜。

本聪老师：对。如果是草莓，说明Bob的资产少于Alice，如果是桃子，说明两人财富相当，是西瓜，说明Bob财富超过了Alice。

小天：嗯，明白了。

本聪老师：这是个算法的最简单示例，帮助大家理解不经意传输的机制。下面我们再介绍隐私计算中零知识证明的一种算法，叫做zk-SNARK。大家谁能说说对零知识证明的理解？

小明：我理解零知识证明，简单来说就是证明者不泄露任何有用信息的前提条件下，使验证者相信某个论断是正确的。

本聪老师：基本如此。举个例子比如这个场景：Alice心中隐藏一组数，x和y的值，她想让Bob相信自己知道这组数，但是不能暴露这组数，不过可以给Bob一点提示，就是X+y=7。当然这个还不足以说明算法。我们再尝试使用zk-SNARK算法机制来模拟实现。我们首先确认一下规则：

假设存在函数E(x)，满足条件：

1、如果x≠y，则E(x)≠E(y)；

2、并且已知E(x)，不能反推出x的值；

3、并且已知E(x)，E(y)，可以计算出E(x+y)的值。

具体计算过程是这样的，如图2-17：

• Alice发送(x+y)的值（7）、E(x)和E(y)给Bob；
• Bob计算E(7)；
• Bob根据收到的E(x)和E(y)，计算E(x+y)；
• Bob接下来验证E(x+y)和E(7)的关系；
• 如果E(x+y)=E(7)，则验证成功，证明Alice未泄露x,y的值，证明了它们的和是7。

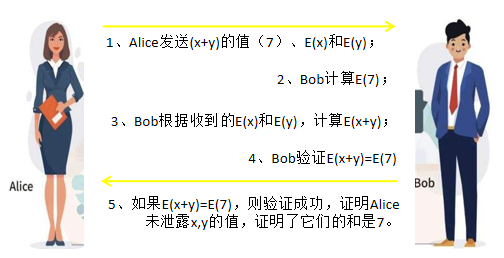
图2-17 zk-SNARK算法机制

小云：看起来好像很简单的样子。

本聪老师：当然真正的算法不是这么简单，实用场景中会复杂许多，比如虽然已知E(x)，不能反推出x的值，但是还是不建议直接暴露E(x)和E(y)的值给Bob，那么可以通过增加偏移变量t的方式实现。那么过程就变为：

Alice产生一个数t, 并把E(x+t)和E(y-t)的数值发给Bob，

Bob通过收到的E(x+t)和E(y-t)计算出E(x+y)的值，

Bob同时计算E(7)的值，如果E(x+y)=E(7)，那么验证通过。

本聪老师：还有x+y=7这个太简单，把这个搞复杂一些，比如变换为多项式P(x)，最后还可以添加随机性，将刚才提到的偏移变量调整为随机偏移多项式R(x)。这样复杂化之后，就可以将zk-SNARK应用到更多真实的场景中了。

本聪老师：基础篇也就是预备知识，我们就介绍完了，下面我们就正式进入去中心化数字身份的学习了。

本文内容摘自《对话去中心化数字身份》。作者：乔布施。首发平台：https://ytm.app

欢迎转载，请注明出处及作者。